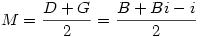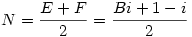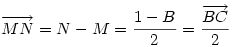| MENU |
| Strona główna |
| Metody |
| - Sinusy |
| - Analityczna |
| - Zespolone |
| Zadanka |
| Rozwiązania |
| Linki |
| O Autorze |
Pragnę przedstawić 3 metody liczenia zadań geometrycznych:
Metoda 1:
SINUSY
Za medium pomiedzy geometrią, a resztą świata niewątpliwie uznać można trzy twierdzenia:
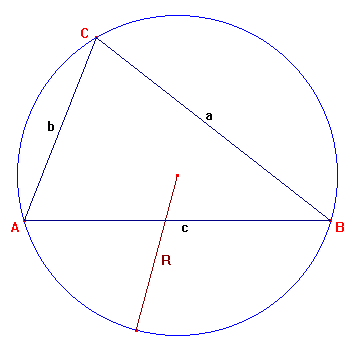
- Pole trójkąta wyraża się wzorem:
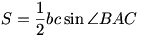
- Twierdzenie Sinusów
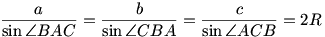
- Twierdzenie Cosinusów

Jak się za to zabrać?
Zasada jest prosta. Staramy się wyrazić długości interesujących nas odcinków i miary interesujących nas kątów za pomocą minimalnej liczby długości innych odcinków i (funkcji trygonometrycznych) innych kątów. Gdzie się da, stosujemy twierdzenie sinusów/cosinusów. Przekształcamy w ten sposób tezę na dowód równaności dwóch wyrażeń. Tu nasz kontakt z geometrią się kończy, a zaczyna biegłość w przekształcaniu funkcji trygonometrycznych oraz standardowych rachunkach.
Przykład (LVII Olimpiada Matematyczna, etap I, zadanie 6.)
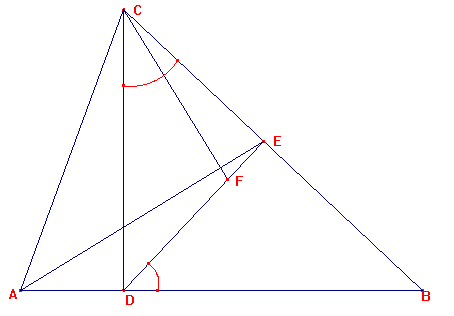
W trójkącie ostrokątnym ABC wysokości przecinają się w punkcie H. Prosta przechodząca przez H przecina odcinki AC i BC odpowiednio w punktach D i E. Prosta przechodząca przez H i prostopadła do prostej DE przecina prostą AB w punkcie F. Dowieść, że
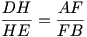
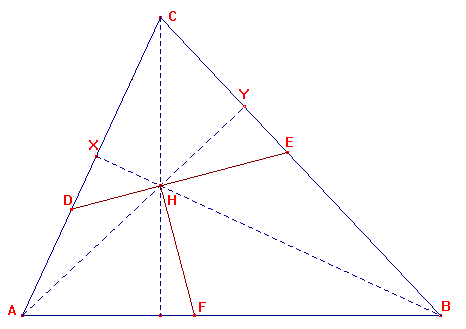
Rozwiązanie:
Oznaczmy przecięcie prostych BH i AC przez X, a przecięcie prostych AH i BC przez Y. Niech
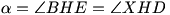 oraz
oraz  . Wówczas
. Wówczas 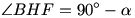 , natomiast
, natomiast 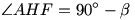 .
.
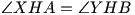 i
i 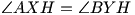 , toteż
, toteż 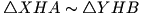 , więc
, więc
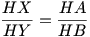
Stąd już otrzymujemy:
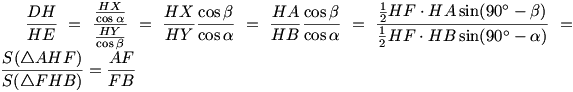
Metoda 2:
GEOMETRIA ANALITYCZNA
Co łączy geometrię z analizą? Podobnie jak w poprzedniej metodzie, będziemy chcieli zmienić geometryczną tezę w dowód równości dwóch liczb, rozwiązanie układu równań, itp. Okazuje się, że każdy obiekt geometryczny da się (w prostszy lub bardziej skomplikowany sposób) opisać równaniami.
Jak się za to zabrać?
Po pierwsze nasz rysunek trzeba umieścić w układzie współrzędnych. Kluczowym jest tutaj wybór początku układu oraz osi współrzędnych. Dobrym zwyczajem jest mianowanie początkiem układu punkt przecięcia największej liczby prostych, środek okręgu, lub punkt przecięcia prostych prostopadłych. Wprowadźmy zmienne określające współrzędne kartezjańskie interesujących nas punktów. Czasami warto użyć współrzędnych biegunowych. Określone relacje geometryczne między punktami chcemy teraz wyrazić w postaci zależności pomiędzy tymi zmiennymi.
Uświadommy sobie następującą fakty:
- Punkty leżą na jednej prostej, jeżeli ich współrzędne x, y spełniają równanie tej samej prostej Ax + By + C = 0. Analogicznie, punkty leżą na okręgu, jeżeli spełniają równanie okręgu (x - a)2 + (y - b)2 = r2.
- Współczynnik kierunkowy prostej (a we wzorze y = ax + b) jest tangensem kąta, jaki prosta tworzy z osią OX.
- Proste są prostopadłe wtedy i tylko wtedy, gdy iloczyn ich współczynników kierunkowych jest równy -1 lub jedna z nich jest pozioma, a druga pionowa.
Przykład (LVI Olimpiada Matematyczna, etap I, zadanie 3.)
W trójkącie ostrokątnym ABC punkt D jest rzutem prostokątnym punktu C na prostą AB. Punkt E jest rzutem prostokątnym punktu D na prostą BC. Punkt F leży na odcinku DE, przy czym
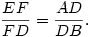
Rozwiązanie:
Wprowadźmy taki układ współrzędnych, że D = (0, 0) oraz B = (1, 0). Ponadto oznaczmy to, co konieczne: Niech C = (0, c) i A = (-a, 0). Wprowadzone wielkości jednoznacznie wyznaczają resztę rysunku. Dlatego współrzędne kolejnych punktów będziemy chcieli wyrazić tylko za pomocą liczb a i c.
Niech Px oznacza współrzędną odciętą punktu P, a Py współrzędną rzędną, dla każdego punktu P.
Niech
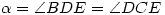 . Tangens tego kąta wynosi 1/c, a zatem współczynnik kierunkowy prostej DE również wynosi 1/c, natomiast współczynnik kierunkowy prostej BC wynosi -c. Tak więc prostą DE opisuje równanie: y = x/c, natomiast prostą BC opisuje równanie: y = c - cx. Punkt E leży na przecięciu tych prostych, więc spełnia oba te równania, a zatem punkt E obliczymy, rozwiązując układ równań:
. Tangens tego kąta wynosi 1/c, a zatem współczynnik kierunkowy prostej DE również wynosi 1/c, natomiast współczynnik kierunkowy prostej BC wynosi -c. Tak więc prostą DE opisuje równanie: y = x/c, natomiast prostą BC opisuje równanie: y = c - cx. Punkt E leży na przecięciu tych prostych, więc spełnia oba te równania, a zatem punkt E obliczymy, rozwiązując układ równań:
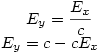
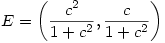
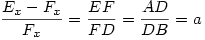
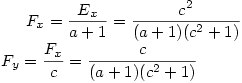
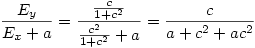
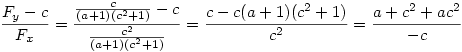
Metoda 3:
LICZBY ZESPOLONE
Liczbę zespoloną a + bi możemy traktować w dwojaki sposób: jako punkt (a, b) lub jako wektor [a, b]. Liczby zespolone dodajemy i odejmujemy tak samo, jak wektory. Warta uwagi jest postać trygonometryczna liczby zespolonej: 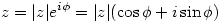 . Liczbę |z| nazywamy modułem, a liczbę
. Liczbę |z| nazywamy modułem, a liczbę 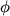 argumentem liczby zespolonej z. Moduł liczby jest długością odpowiadającego jej wektora, a argument kątem, jaki wektor ten tworzy z osią OX. Stąd wniosek, że jeżeli
argumentem liczby zespolonej z. Moduł liczby jest długością odpowiadającego jej wektora, a argument kątem, jaki wektor ten tworzy z osią OX. Stąd wniosek, że jeżeli 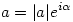 , a
, a 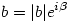 , to
, to 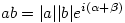 . W szczególności, pomnożenie przez liczbę o module 1 i argumencie
. W szczególności, pomnożenie przez liczbę o module 1 i argumencie 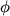 to dodanie do argumentu
to dodanie do argumentu 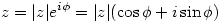 . W jeszcze większej szczególności, pomnożenie przez i jest obrotem o kąt prosty, a pomnożenie przez
. W jeszcze większej szczególności, pomnożenie przez i jest obrotem o kąt prosty, a pomnożenie przez 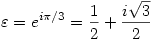 obrotem o 60 stopni. Liczby
obrotem o 60 stopni. Liczby 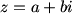 i
i 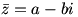 nazywamy liczbami sprzężonymi. Są one symetryczne względem osi OX. Godnym zapamiętania jest też fakt, że średnią arytmetyczną wierzchołków wielokąta jest jego środek ciężkości. W szczególności, średnią arytmetyczną liczb A i B jest środek odcinka AB.
nazywamy liczbami sprzężonymi. Są one symetryczne względem osi OX. Godnym zapamiętania jest też fakt, że średnią arytmetyczną wierzchołków wielokąta jest jego środek ciężkości. W szczególności, średnią arytmetyczną liczb A i B jest środek odcinka AB.
Jak się za to zabrać?
Zasada jest bardzo podobna do geometrii analitycznej: oznaczamy punkty liczbami zespolonymi, wyrażamy jedne przez drugie i przekształcamy w ten sposób tezę na dowód równości dwóch wyrażeń. Warto pamiętać o zasadzie: Okrąg łatwo opisać liczbami zespolonymi, trudno analitycznie, prostą natomiast łatwo opisać analitycznie, a ciężko liczbami zespolonymi. Kwadraty, trójkąty zbudowane na bokach wielokąta sugerują rozwiązanie korzystające z liczb zespolonych (kwadrat to pomnożenie jednego boku przez i, a trójkąt równoboczny, to pomnożenie jednego boku przez  ).
).
Przykład (LIII Olimpiada Matematyczna, etap I, zadanie 2.)
Na bokach AB i AC trójkąta ABC zbudowano, po jego zewnętrznej stronie, kwadraty ABDE i ACFG. Punkty M i N są odpowiednio środkami odcinków DG i EF. Wyznaczyć możliwe wartości wyrażenia MN:BC.
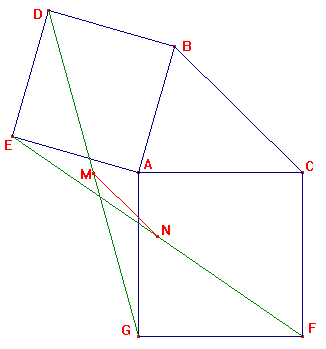
Rozwiązanie:
Wprowadźmy taki układ współrzędnych, że A = 0 oraz C = 1. Wówczas D = B + Bi, natomiast G = -i. Stąd: